New mathematical model captures forces involved in cell movement

Berlin-based theoretical physicists and Munich-based experimental physicists have teamed up to find out the precise mechanisms that play a crucial role in cell motility. The results were published in the journal, Proceedings of the National Academy of Sciences (PNAS).

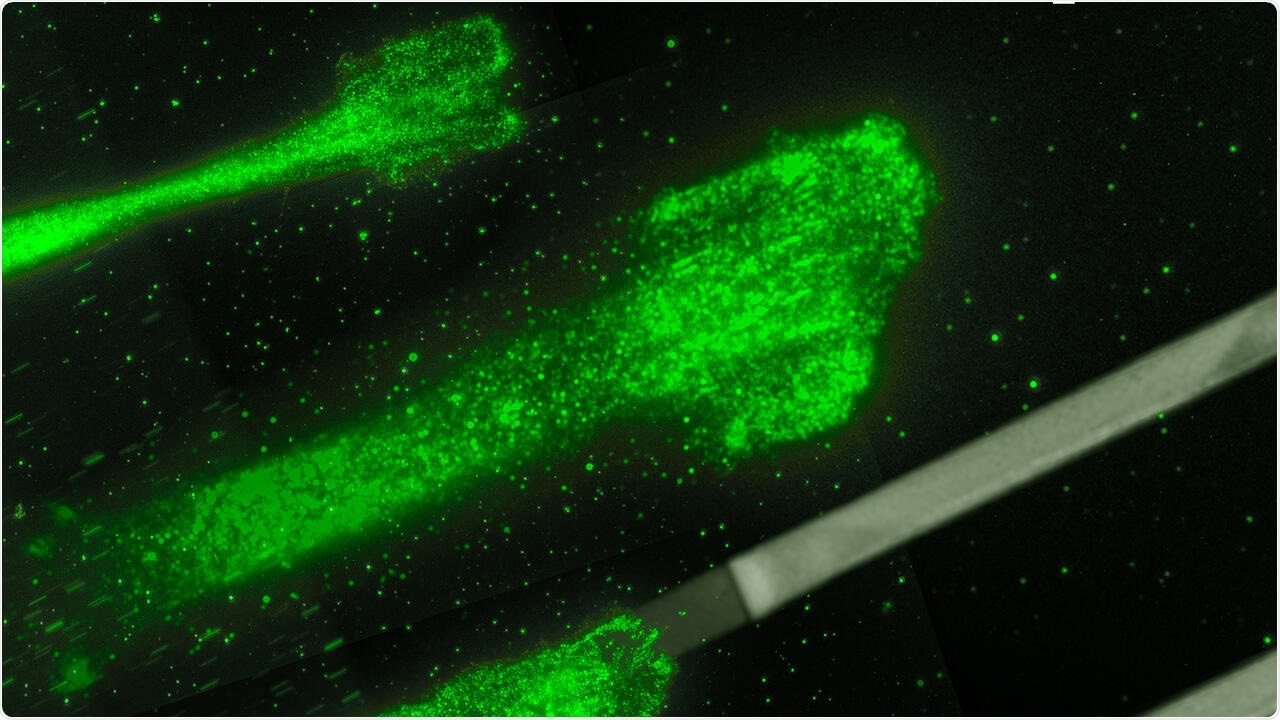
Cancer cells moving on glycoproteine strips: These strips act like splints, which allow to control and to study the movement of the cells better. Image Credit: © Rädler Lab, Ludwig Maximilians Universität München.

Researchers are aware that cell velocity, or how rapidly a cell moves, relies on the level of the stickiness of the underlying surface; however, the actual mechanics of this association have continued to be elusive for many years.

Now, scientists from the Max Delbrück Center for Molecular Medicine in the Helmholtz Association (MDC) and Ludwig Maximilians Universität München (LMU) have determined the precise mechanisms and designed a mathematical model that captures the forces that contribute to the movement of cells. These findings shed new light on the developmental biology and promising treatments for cancer.

Cell movement is an underlying process, which is particularly crucial at the time of development when cells normally differentiate into their target cell type and subsequently shift to the right tissue. In addition to this, cells also migrate to repair wounds, whereas cancer cells move to the closest blood vessel to spread to other body parts.

The mathematical model we developed can now be used by researchers to predict how different cells will behave on various substrates. Understanding these basic movements in precise detail could provide new targets to interrupt tumor metastasis.”

Martin Falcke, Professor and Head, Mathematical Cell Physiology Lab, Max Delbrück Center for Molecular Medicine in the Helmholtz Association

Professor Falcke has also co-headed the study.

Teaming up to pin down

This discovery resulted from the collaboration between experimental physicists from LMU and theoretical physicists from MDC.

Headed by Professor Joachim Rädler, the experimentalists tracked the rapid movement of over 15,000 cancer cells along constricted lanes on a sticky surface, in which the stickiness changed between high and low. This enabled the researchers to visualize what exactly occurs when the cell moves between levels of stickiness, which is more indicative of the dynamic environment within the body.

Falcke and Behnam Amiri, the co-first author of the study and Ph.D. student in Falcke’s laboratory then applied the huge dataset to design a mathematical equation that records the elements shaping the movement of cells.

Previous mathematical models trying to explain cell migration and motility are very specific, they only work for one feature or cell type. What we tried to do here is keep it as simple and general as possible.”

Behnam Amiri, Study Co-First Author and PhD Student, Max Delbrück Center for Molecular Medicine in the Helmholtz Association

The new method worked much better than anticipated: the model corresponded with the information collected at LMU and held true for measurements relating to many other types of cells collected over the last three decades.

“This is exciting,” Falcke added. “It’s rare that you find a theory explaining such a large spectrum of experimental results.”

Friction is key

Whenever a cell migrates, it tends to push out its membrane in the direction it travels—extending an internal network of actin filaments as it moves—and subsequently peels off its back end. But how rapidly this occurs is governed by adhesion bonds that develop between the cell and its underlying surface. In the absence of bonds, the cell can barely travel because the network of actin filaments does not have anything to push off against.

The reason can be attributed to friction: “When you are on ice skates you cannot push a car, only when there is enough friction between your shoes and the ground can you push a car,” added Falcke.

When the number of bonds increases, more friction is created. This causes the cell to produce more force and travel faster, until it becomes so sticky at one point that it turns out to be relatively harder to pull off the back end, thereby slowing down the cell again.

Slow, but not stuck

The team studied what exactly occurs when the back and front ends of the cell experience varying degrees of stickiness. The researchers were specifically curious to find out what precisely occurs when it is stickier under the cell’s rear end than the front because that is when the cell could possibly get stuck and cannot create sufficient force to pull off the back end.

This could have been the case, provided the adhesion bonds resembled screws, keeping the cell to the substrate. Although Falcke and Amiri had initially included this type of “elastic” force in their new model, the equation only worked with friction forces.

“For me, the most challenging part was to wrap my mind around this mechanism working only with friction forces,” Falcke added. This is because the cell does not have anything to strongly bind to. However, it is the friction-like forces that enable the cell to continue its movement, even when bonds are relatively stronger in the rear than the front, slowly peeling itself off, similar to a scotch tape.

Even if you pull just a little with a weak force, you are still able to peel the tape off—very slowly, but it comes off. This is how the cell keeps itself from getting stuck.”

Martin Falcke, Professor and Head, Mathematical Cell Physiology Lab, Max Delbrück Center for Molecular Medicine in the Helmholtz Association

At present, the researchers are investigating how cells migrate in two dimensions, for example, how they make hard right and left turns, and even U-turns.